Совместное решение образец

Кадровое делопроизводство -> 3.3.6. РЕШЕНИЕ 3.3.6. РЕШЕНИЕ

Решение - распорядительный документ коллегиального органа управления. Издается министерствами, ведомственными, научными советами.

Решения издают организации (при коллегиальном управлении и при единоначалии), государственные органы и общественные организации.

Текст решения состоит из констатирующей и распорядительной частей.

В констатирующей части указывают причины издания решения, цели, которые должны быть достигнуты при его выполнении. Если решение издают на основании распорядительного документа вышестоящего органа, то в констатирующей части указывают название, номер, дату, заголовок этого распорядительного документа.

В распорядительной части указывают наименование органа, принимающего решение, затем пишут слово РЕШИЛ прописными буквами на отдельной строке.

Распорядительную часть можно делить на пункты, где указывают исполнителя (организацию, структурное подразделение, должностное лицо) - действие - срок исполнения.

Решение подписывает председатель и секретарь коллегиального органа. При этом они не вправе менять содержание текста.

Решение оформляется на бланках формата А4.

Формуляр-образец РЕШЕНИЯ состоит из реквизитов:

- наименование организации - автора документа;

- наименование вида документа - РЕШЕНИЕ;

- дата (принятие решения на заседании коллегиального органа), номер;

- заголовок к тексту;

- подпись (председателя, секретаря);

- визы согласования (составителя, руководителя подразделения, вносящего проект решения, исполнителей, юрисконсульта, должностных лиц, ответственных за исполнение решения);

- отметка об исполнении документа и направлении его в дело.

Особенности программы: гибкое штатное расписание без ограничения уровня вложенности с возможностью включения филиалов с собственной структурой;импорт и экспорт данных по сотрудникам из программ 1С (Бухгалтерия, Зарплата и Кадры, Комплексная и т.д.);сохранение приказов и отчетов в редактируемых форматах XLS, DOC или ODT, ODS (независимо от того, установлен у Вас Microsoft Office или Open Office);табель учета рабочего времени, автоматически формирующийся на основании существующих приказов по сотруднику и графику его работы. Табель имеет удобный интерфейс редактирования и ввода отработанных часов. Все изменения, внесённые в табель, сразу отражаются в документообороте в виде соответствующих приказов;возможность хранения внутри программы внешних документов в различных форматах (Word, Excel, изображения и т.д.);возможность приёма нескольких сотрудников с различными ставками на одну штатную единицу;возможность работы одного сотрудника на различных должностях в рамках одной организации на различных ставках;

Удобная и простая программа кадрового учёта, позволяющая автоматически формировать большинство кадровых документов (штатное расписание, личная карточка, приказы, отчёты для ПФР). Основные возможности программы "Отдел кадров": хранение в базе личных данных о каждом сотруднике, расчёт общего стажа, непрерывного стажа и стажа работы на данном предприятии, учёт отпусков, учёт командировок, отпусков и поощрений. Автоматическое составление штатного расписания, личной карточки и всех кадровых приказов.

Программа имеет следующие преимущества по сравнению с программой "Отдел кадров 6.0":не требует наличия установленного Microsoft Access, программа "Отдел кадров плюс" полностью автономна;программа позволяет сохранять все приказы и отчёты в формате Excel;программа позволяет вести полноценный табельный учет по форме Т-12;программа хранит и отображает структуру предприятия в удобной древовидной форме.

Программа разработана для помощи кадровикам при расчёте стажа. По записям в трудовой книжке производится расчёт общего и непрерывного стажа сотрудников. Все расчёты, производимые пользователем автоматически сохраняются в базе данных. Таким образом программа представляет собой электронную картотеку трудовых книжек сотрудников. Программа имеет полностью заполненный справочник статей увольнения согласно новому Трудовому Кодексу. Интерфейс пользователя программы интуитивно понятный, и для работы с программой не требуется глубоких знаний по работе с персональным компьютером. Также программа имеет функцию вывода на печать отчёта о стаже сотрудников.

Программа позволяет вести учет внутренних документов, входящей и исходящей корреспонденции (факсы, e-mail, почтовые письма и т.д.). Вы сможете назначать список ответственных за согласование входящих документов с последующим отслеживанием статуса с уведомлением о дате согласования. Программа может привязать к документу неограниченное количество вложенных файлов любого формата (отсканированный факс, файлы MS Word, MS Excel и т.д.), вести структурированые справочники по сотрудникам (согласователи и исполнители), организациям (получатели и отправители), формировать наглядные отчеты по внутренним документам (вести журнал документов по организации) и корреспонденции, производить поиск необходимого документа по одному или нескольким реквизитам (номер, тип, дата создания и т.д.)

Программа предназначена для автоматизации работы с договорами. Необходимость учета договоров возникает в тот момент, когда с помощью обычного журнала договоров, таблицы Excel или справочника учетной системы невозможно составить ясную картину договорной деятельности, планировать и контролировать расчеты и сроки работ по договорам.Программа "Документ плюс" уменьшает рутинную и однообразную работу по подготовке и согласованию договоров, расчетам и позволяет быстро получать оперативную и аналитическую информацию по договорам, связанным с ними работам и операциям.

Программа служит для автоматизации торговых операций (формирование документов), работы с клиентами (CRM) и формирования отчетности по торговой деятельности (аналитика).Функции: управление контактами, история взаимодействия с клиентами; управление рабочим временем; автоматизация документооборота; аналитика; функциональные инструменты.

Программа для автоматизации журнала приказов учебного учреждения. Программа формирует реестр специальностей, курсов, групп, студентов и приказов (выписок). Внедрение программы позволяет сэкономить время на формирование приказов (выписок) и повышает эффективность ведения журнала приказов в учебном заведении. Программа автоматически формирует приказ о зачислении, приказ о переводе на следующий курс, приказ об оплате за обучение по индивидуальному плану, приказ о переводе студентов на ускоренную форму обучения, приказ о предоставлении академического отпуска, приказ о восстановлении в число студентов, приказ об отчислении, приказ о допуске к защите дипломных работ и сдаче итоговых государственных экзаменов и другие приказы

Все программы (Отдел кадров 6.0, Отдел кадров плюс, Отдел кадров 2015, Расчёт стажей, ДокПартнёр, Документ Плюс, Клиент Плюс, Журнал приказов. Образование) одним архивом.

Решение _пример оформления по ГОСТу

О подготовке к пушному

аукциону в Санкт-Петербурге

На основании координационного плана от 00.00.98 Совет директоров ассоциации "Российская пушнина"

1. Назначить ответственным представителем ЗАО на аукционе Васильева А.Д.

2. Васильеву А.Д. подготовить предложения по составу делегации и представить на рассмотрение Совету до 00.00.2000г.

3. Смирнову Л.В. подготовить уточненный ассортимент пушных изделий, пользующихся наибольшим спросом, и представить на рассмотрение Совету до 00.00.2000г.

Председатель Совета подпись А.Л.Шилов

Члены Совета подпись Л.А.Горбунов

Отметка об исполнителе

Решение представляет собой документ коллегиального органа (совета директоров, общего собрания акционеров и т. п.), составляемый по производственным вопросам.

Решения оформляются аналогично другим распорядительным документам с использованием слов "РЕШИЛ" или "РЕШИЛИ". Подписываются решения председателем и всеми членами коллегиального органа или председателем и секретарем.

"АРМ Секретаря", ООО "ИКК "Гарант Интернэшнл", 1999, E-Mail: offex@icc.spb.su

Несовместные системы и системы с общим решением

Продолжаем разбираться с системами линейных уравнений. До сих пор я рассматривал системы, которые совместны и имеют единственное решение. Такие системы можно решить любым способом: методом подстановки («школьным»), по формулам Крамера, матричным методом . методом Гаусса . Однако на практике широко распространены еще два случая:

– Система несовместна (не имеет решений);
– Система совместна и имеет бесконечно много решений.

Примечание: термин «совместность» подразумевает, что у системы существует хоть какое-то решение. В ряде задач требуется предварительно исследовать систему на совместность, как это сделать – см. статью о ранге матриц .

Для этих систем применяют наиболее универсальный из всех способов решения – метод Гаусса. На самом деле, к ответу приведет и «школьный» способ, но в высшей математике принято использовать гауссовский метод последовательного исключения неизвестных. Те, кто не знаком с алгоритмом метода Гаусса, пожалуйста, сначала изучите урок метод Гаусса для чайников .

Сами элементарные преобразования матрицы – точно такие же. разница будет в концовке решения. Сначала рассмотрим пару примеров, когда система не имеет решений (несовместна).

Решить систему линейных уравнений

Что сразу бросается в глаза в этой системе? Количество уравнений – меньше, чем количество переменных. Если количество уравнений меньше, чем количество переменных. то сразу можно сказать, что система либо несовместна, либо имеет бесконечно много решений. И это осталось только выяснить.

Начало решения совершенно обычное – запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) На левой верхней ступеньке нам нужно получить +1 или –1. Таких чисел в первом столбце нет, поэтому перестановка строк ничего не даст. Единицу придется организовать самостоятельно, и сделать это можно несколькими способами. Я поступил так: К первой строке прибавляем третью строку, умноженную на –1.

(2) Теперь получаем два нуля в первом столбце. Ко второй строке прибавляем первую строку, умноженную на 3. К третьей строке прибавляем первую строку, умноженную на 5.

(3) После выполненного преобразования всегда целесообразно посмотреть, а нельзя ли упростить полученные строки? Можно. Вторую строку делим на 2, заодно получая нужную –1 на второй ступеньке. Третью строку делим на –3.

(4) К третьей строке прибавляем вторую строку.

Наверное, все обратили внимание на нехорошую строку, которая получилась в результате элементарных преобразований: . Ясно, что так быть не может. Действительно, перепишем полученную матрицу обратно в систему линейных уравнений:

Если в результате элементарных преобразований получена строка вида , где – число, отличное от нуля, то система несовместна (не имеет решений) .

Как записать концовку задания? Нарисуем белым мелом: «в результате элементарных преобразований получена строка вида , где » и дадим ответ: система не имеет решений (несовместна).

Если же по условию требуется ИССЛЕДОВАТЬ систему на совместность, тогда необходимо оформить решение в более солидном стиле с привлечением понятия ранга матрицы и теоремы Кронекера-Капелли .

Обратите внимание, что здесь нет никакого обратного хода алгоритма Гаусса – решений нет и находить попросту нечего.

Решить систему линейных уравнений

Это пример для самостоятельного решения. Полное решение и ответ в конце урока. Снова напоминаю, что ваш ход решения может отличаться от моего хода решения, у алгоритма Гаусса нет сильной «жёсткости».

Еще одна техническая особенность решения: элементарные преобразования можно прекращать сразу же. как только появилась строка вида , где . Рассмотрим условный пример: предположим, что после первого же преобразования получилась матрица . Матрица еще не приведена к ступенчатому виду, но в дальнейших элементарных преобразованиях нет никакой необходимости, так как появилась строка вида , где . Следует сразу дать ответ, что система несовместна.

Когда система линейных уравнений не имеет решений – это почти подарок, ввиду того, что получается короткое решение, иногда буквально в 2-3 действия.

Но всё в этом мире уравновешено, и задача, в которой система имеет бесконечно много решений – как раз длиннее.

Решить систему линейных уравнений

Тут 4 уравнений и 4 неизвестных, таким образом, система может иметь либо единственное решение, либо не иметь решений, либо иметь бесконечно много решений. Как бы там ни было, но метод Гаусса в любом случае приведет нас к ответу. В этом его и универсальность.

Начало опять стандартное. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Вот и всё, а вы боялись.

(1) Обратите внимание, что все числа в первом столбце делятся на 2, поэтому на левой верхней ступеньке нас устраивает и двойка. Ко второй строке прибавляем первую строку, умноженную на –4. К третьей строке прибавляем первую строку, умноженную на –2. К четвертой строке прибавляем первую строку, умноженную на –1.

Внимание! У многих может возникнуть соблазн из четвертой строки вычесть первую строку. Так делать можно, но не нужно, опыт показывает, что вероятность ошибки в вычислениях увеличивается в несколько раз. Только складываем: К четвертой строке прибавляем первую строку, умноженную на –1 – именно так!

(2) Последние три строки пропорциональны, две из них можно удалить.

Здесь опять нужно проявить повышенное внимание. а действительно ли строки пропорциональны? Для перестраховки (особенно, чайнику) не лишним будет вторую строку умножить на –1, а четвертую строку разделить на 2, получив в результате три одинаковые строки. И только после этого удалить две из них.

В результате элементарных преобразований расширенная матрица системы приведена к ступенчатому виду: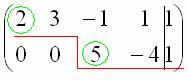

При оформлении задачи в тетради желательно для наглядности делать такие же пометки карандашом.

Перепишем соответствующую систему уравнений:

«Обычным» единственным решением системы здесь и не пахнет. Нехорошей строки тоже нет. Значит, это третий оставшийся случай – система имеет бесконечно много решений. Иногда по условию нужно исследовать совместность системы (т.е. доказать, что решение вообще существует), об этом можно прочитать в последнем параграфе статьи Как найти ранг матрицы? Но пока разбираем азы:

Бесконечное множество решений системы коротко записывают в виде так называемого общего решения системы .

Общее решение системы найдем с помощью обратного хода метода Гаусса.

Сначала нужно определить, какие переменные у нас являются базисными. а какие переменные свободными. Не обязательно заморачиваться терминами линейной алгебры, достаточно запомнить, что вот существуют такие базисные переменные и свободные переменные.

Базисные переменные всегда «сидят» строго на ступеньках матрицы .
В данном примере базисными переменными являются и

Свободные переменные – это все оставшиеся переменные, которым не досталось ступеньки. В нашем случае их две: – свободные переменные.

Теперь нужно всебазисные переменные выразить только черезсвободные переменные .

Обратный ход алгоритма Гаусса традиционно работает снизу вверх.
Из второго уравнения системы выражаем базисную переменную :

Теперь смотрим на первое уравнение: . Сначала в него подставляем найденное выражение :

Осталось выразить базисную переменную через свободные переменные :

В итоге получилось то, что нужно – все базисные переменные ( и ) выражены только через свободные переменные :

Собственно, общее решение готово:

Как правильно записать общее решение?
Свободные переменные записываются в общее решение «сами по себе» и строго на своих местах. В данном случае свободные переменные 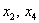следует записать на второй и четвертой позиции:
.

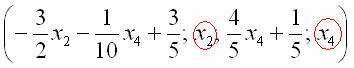Придавая свободным переменным произвольные значения. можно найти бесконечно много частных решений. Самыми популярными значениями являются нули, поскольку частное решение получается проще всего. Подставим в общее решение:

– частное решение.

Другой сладкой парочкой являются единицы, подставим в общее решение:

– еще одно частное решение.

Легко заметить, что система уравнений имеет бесконечно много решений (так как свободным переменным мы можем придать любые значения)

Каждое частное решение должно удовлетворять каждому уравнению системы. На этом основана «быстрая» проверка правильности решения. Возьмите, например, частное решение и подставьте его в левую часть каждого уравнения исходной системы:

Всё должно сойтись. И с любым полученным вами частным решением – тоже всё должно сойтись.

Но, строго говоря, проверка частного решения иногда обманывает, т.е. какое-нибудь частное решение может удовлетворять каждому уравнению системы, а само общее решение на самом деле найдено неверно.

Поэтому более основательна и надёжна проверка общего решения. Как проверить полученное общее решение ?

Это несложно, но довольно муторно. Нужно взять выражения базисных переменных, в данном случае и , и подставить их в левую часть каждого уравнения системы.

В левую часть первого уравнения системы:

Получена правая часть исходного уравнения.

В левую часть второго уравнения системы:

Получена правая часть исходного уравнения.

И далее – в левые части третьего и четвертого уравнение системы. Это дольше, но зато гарантирует стопроцентную правильность общего решения. Кроме того, в некоторых заданиях требуют проверку общего решения.

Решить систему методом Гаусса. Найти общее решение и два частных. Сделать проверку общего решения.

Это пример для самостоятельного решения. Здесь, кстати, снова количество уравнений меньше, чем количество неизвестных, а значит, сразу понятно, что система будет либо несовместной, либо с бесконечным множеством решений. Что важно в самом процессе решения? Внимание, и еще раз внимание. Полное решение и ответ в конце урока.

И еще пара примеров для закрепления материала

Решить систему линейных уравнений. Если система имеет бесконечно много решений, найти два частных решения и сделать проверку общего решения

Решение. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) Ко второй строке прибавляем первую строку. К третьей строке прибавляем первую строку, умноженную на 2. К четвертой строке прибавляем первую строку, умноженную на 3.
(2) К третьей строке прибавляем вторую строку, умноженную на –5. К четвертой строке прибавляем вторую строку, умноженную на –7.
(3) Третья и четвертая строки одинаковы, одну из них удаляем.

Обратный ход:
Выразим базисные переменные через свободную переменную:
Из третьего уравнения:

Рассмотрим второе уравнение и подставим в него найденное выражение :

Рассмотрим первое уравнение и подставим в него найденные выражения и :

Да, всё-таки удобен калькулятор, который считает обыкновенные дроби.

Таким образом, общее решение:

Еще раз, как оно получилось? Свободная переменная одиноко сидит на своём законном четвертом месте. Полученные выражения для базисных переменных , тоже заняли свои порядковые места.

Сразу выполним проверку общего решения. Работа для негров, но она у меня уже выполнена, поэтому ловите =)

Подставляем трех богатырей , , в левую часть каждого уравнения системы:

Получены соответствующие правые части уравнений, таким образом, общее решение найдено верно.

Теперь из найденного общего решения получим два частных решения. Шеф-поваром здесь выступает единственная свободная переменная . Ломать голову не нужно.

Пусть , тогда – частное решение.
Пусть , тогда – еще одно частное решение.

Ответ. Общее решение: , частные решения: , .

Зря я тут про негров вспомнил. потому что в голову полезли всякие садистские мотивы и вспомнилась известная фотожаба, на которой куклуксклановцы в белых балахонах бегут по полю за чернокожим футболистом. Сижу, тихо улыбаюсь. Знаете, как отвлекает….

Много математики вредно, поэтому похожий заключительный пример для самостоятельного решения.

Найти общее решение системы линейных уравнений.

Проверка общего решения у меня уже сделана, ответу можно доверять. Ваш ход решения может отличаться от моего хода решения, главное, чтобы совпали общие решения.

Наверное, многие заметили неприятный момент в решениях: очень часто при обратном ходе метода Гаусса нам пришлось возиться с обыкновенными дробями. На практике это действительно так, случаи, когда дробей нет – встречаются значительно реже. Будьте готовы морально, и, самое главное, технически.

Остановлюсь на некоторых особенностях решения, которые не встретились в прорешанных примерах.

В общее решение системы иногда может входить константа (или константы), например: . Здесь одна из базисных переменных равна постоянному числу: . В этом нет ничего экзотического, так бывает. Очевидно, что в данном случае любое частное решение будет содержать пятерку на первой позиции.

Редко, но встречаются системы, в которых количество уравнений больше количества переменных. Метод Гаусса работает в самых суровых условиях, следует невозмутимо привести расширенную матрицу системы к ступенчатому виду по стандартному алгоритму. Такая система может быть несовместной, может иметь бесконечно много решений, и, как ни странно, может иметь единственное решение.

И, конечно, повторюсь в своем совете – чтобы комфортно себя чувствовать при решении системы методом Гаусса, следует набить руку и прорешать хотя бы десяток систем.

Решения и ответы:

Пример 2: Решение. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

Выполненные элементарные преобразования:
(1) Первую и третью строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –6. К третьей строке прибавили первую строку, умноженную на –7.
(3) К третьей строке прибавили вторую строку, умноженную на –1.
В результате элементарных преобразований получена строка вида , где , значит, система несовместна.
Ответ. решений нет.

Пример 4: Решение. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на 2. К третьей строке прибавили первую строку, умноженную на 3.

Для второй ступеньке нет единицы, и преобразование (2) направлено на её получение.

(2) К третьей строке прибавили вторую строку, умноженную на –3.
(3) Вторую с третью строки поменяли местами (переставили полученную –1 на вторую ступеньку)
(4) К третьей строке прибавили вторую строку, умноженную на 3.
(5)У первых двух строк сменили знак (умножили на –1), третью строку разделили на 14.

Обратный ход.
– базисные переменные (те, которые на ступеньках), – свободные переменные (те, кому не досталось ступеньки).

Выразим базисные переменные через свободные переменные:
Из третьего уравнения:

Рассмотрим второе уравнение:
Подставим в него найденное выражение :

Рассмотрим первое уравнение:
Подставим в него найденные выражения: , :

Найдем два частных решения
Если , то
Если , то

Проверка: подставим найденное решение (выражения базисных переменных , и ) в левую часть каждого уравнения системы:

Получены соответствующие правые части, таким образом, общее решение найдено верно.

Пример 6: Решение. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) Ко второй строке прибавляем первую строку, умноженную на 2. К третьей строке прибавляем первую строку, умноженную на –2. К четвертой строке прибавляем первую строку, умноженную на –3.
(2) К третьей строке прибавляем вторую строку. К четвертой строке прибавляем вторую строку.
(3) Третья и четвертая строки пропорциональны, одну из них удаляем.

– базисные переменные, – свободная переменная. Выразим базисные переменные через свободную переменную:

Автор: Емелин Александр

(Переход на главную страницу)

Качественные работы без плагиата – Zaochnik.com